2657. Find the Prefix Common Array of Two Arrays

[Problem]

Hash Table Array Bit Manipulation

---

Intuition

• Given two 0-indexed integer permutations A and B of length n, we aim to find a prefix common array C.

• The problem essentially requires us to track common elements between the prefixes of A and B as we iterate through the arrays. The challenge lies in efficiently keeping track of these common elements.

• We know that the there are n elements from 1 to n that all appear once.

Tips:

1. Leverage the Range of Numbers:
   • When the numbers are restricted to a specific range, such as 1 to n, consider using arrays or bit manipulation to efficiently track and count occurrences.
   • Avoid over-complicating with data structures like Set unless absolutely necessary, we will discuss how the set approach works slower compared to the BitSet or Frequency array approach in this scenario.
2. Utilize Small Constraints:
   • Analyze the constraints carefully. For instance, in this problem:
     • n <= 50: A small constraint allows more flexibility in choosing approaches, including less optimized ones.
     • Try to use constant-sized data structures like Arrays work well for small ranges.
     • A BitSet uses individual bits (0 or 1) to represent whether element is present or absent, making it memory-efficient compared to other data structures like Set.
3. Optimize Space Usage:
   • If the constraint ensures a small range, you can often replace sets or hash maps with arrays to save space and improve runtime.
   • For example, replacing a Set with a frequency array (or BitSet also in this case) is a common optimization.

Approach

1. Using HashSet

• Maintain two sets, setA and setB, to store elements seen so far in A and B.
• At each index i, count the number of elements in setA that also exist in setB.
• Update the result array C with this count.

Code

class Solution {
    public int[] findThePrefixCommonArray(int[] A, int[] B) {
        int n = A.length;
        int[] C = new int[n]; // result array

        Set<Integer> setA = new HashSet<>(); // track elements seen in A
        Set<Integer> setB = new HashSet<>(); // track elements seen in B

        for (int i = 0; i < n; i++) {
            setA.add(A[i]); // add current element from A to setA
            setB.add(B[i]); // add current element from B to setB

            int common = 0; // counter for common elements

            // count common elements between setA and setB
            for (int elemA : setA) {
                if (setB.contains(elemA)) {
                    common += 1;
                }
            }

            C[i] = common;
        }
        return C; 
    }
}

2. Using BitSet

• Use a BitSet to efficiently track the presence of elements.
• Represent elements from A and B using specific bit positions: odd for A[i] and even for B[i].
• Check if the bits are set and increment common accordingly.
• More about BitSet

Index Mapping

• For an element x:
  • Odd index (2 * x - 1): Tracks if x has been seen in array A.
  • Even index (2 * x): Tracks if x has been seen in array B.
• This mapping creates a predictable pattern for bit positions, as shown below:

Element (x)	Bit Index for A (2x-1)	Bit Index for B (2x)
1	1	2
2	3	4
3	5	6
4	7	8
…	…	…

• An example is below

For e.g. 
                 A1  B1  A2  B2  A3  B3  A4  B4
index    =>   0   1   2   3   4   5   6   7   8   
bitset   =>   0   1   1   1   0   1   0   1   1


A1 : 1 in array A  |  B1 : 1 in array B
A2 : 2 in array A  |  B2 : 2 in array B


=> Interpretation: If bit at B2(index 4) is `0` means 2 has NOT been seen in the array `B`, vice-versa for `1`.  

• Dry running an example:

For `A = [1, 2, 3]` and `B = [3, 1, 2]`:

Start 
------------------------------------------------
i=0
  
  - `A[0] = 1`: Set bit `1` (odd).
  - `B[0] = 3`: Set bit `6` (even).
------------------------------------------------

i=1
  - `A[1] = 2`: Set bit `3` (odd).
  - `B[1] = 1`: Set bit `2` (even); bit `1` (odd) is already set (common element).

------------------------------------------------

i=2
  - `A[2] = 3`: Set bit `5` (odd); bit `6` (even) is already set (common element).
  - `B[2] = 2`: Set bit `4` (even); bit `3` (odd) is already set (common element).

------------------------------------------------

Output
C = [0, 1, 3]

Code

class Solution {
    public int[] findThePrefixCommonArray(int[] A, int[] B) {
        int n = A.length;
        int[] C = new int[n]; // result array

        // BitSet to track seen elements (size 2*50 + 1), constraints specify max length is 50
        BitSet bs = new BitSet(101); 

        int common = 0; // counter for common elements

        for (int i = 0; i < n; i++) {
            int aa = A[i]; // current element from A
            int bb = B[i]; // current element from B

            // mark A[i] in BitSet (odd index)
            bs.set((2 * aa) - 1);
            if (bs.get(2 * aa)) { // check if B[i] already set
                common++;
            }

            // Mark B[i] in BitSet (even index)
            bs.set(2 * bb);
            if (bs.get((2 * bb) - 1)) { // check if A[i] already set
                common++;
            }

            C[i] = common;
        }
        return C;
    }
}

3. Using Frequency Array

• Use a frequency array to count occurrences of elements in both A and B.
• Whenever an element’s frequency becomes 2 (it means that element appeared in both arrays), increment common.

Code

class Solution {
    public int[] findThePrefixCommonArray(int[] A, int[] B) {
        int n = A.length;
        int[] C = new int[n]; // result array
        int[] freq = new int[n + 1]; // frequency array to track element occurrences

        int common = 0; // counter for common elements

        for (int i = 0; i < n; i++) {
            // increment frequency for A[i]
            freq[A[i]]++;
            if (freq[A[i]] == 2) { // element appears in both arrays
                common++;
            }

            // increment frequency for B[i]
            freq[B[i]]++;
            if (freq[B[i]] == 2) { // element appears in both arrays
                common++;
            }

            C[i] = common;
        }
        return C;
    }
}

Complexity Analysis

Approach	Time Complexity	Space Complexity	Runtime
Using Set	O(n²)	O(n)
Using BitSet	O(n)	O(1)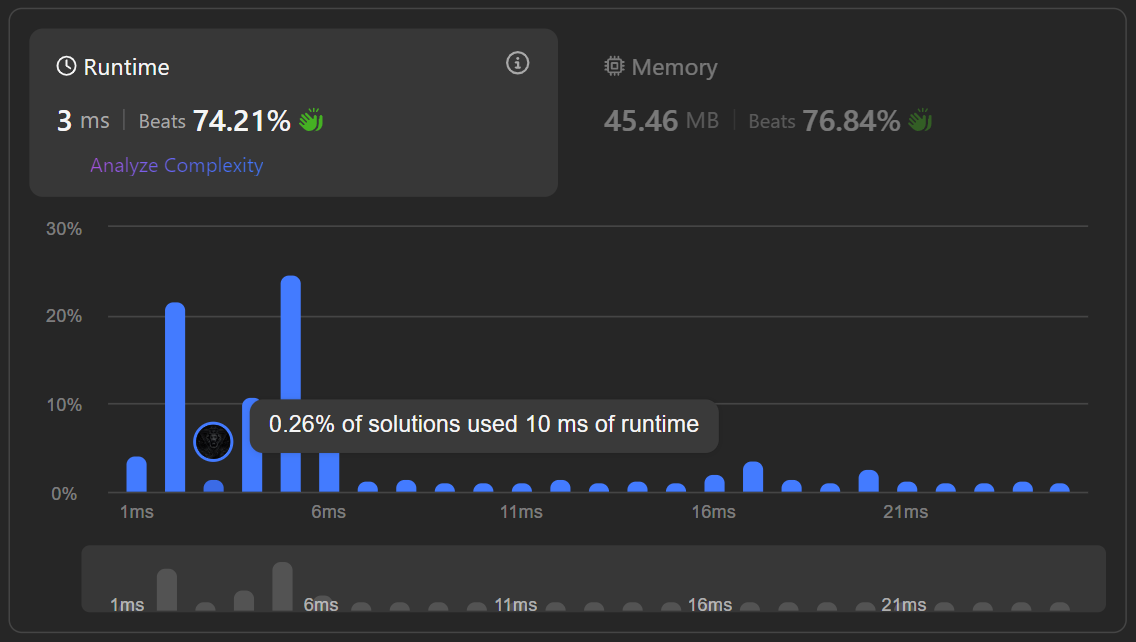
Using Frequency Array	O(n)	O(n)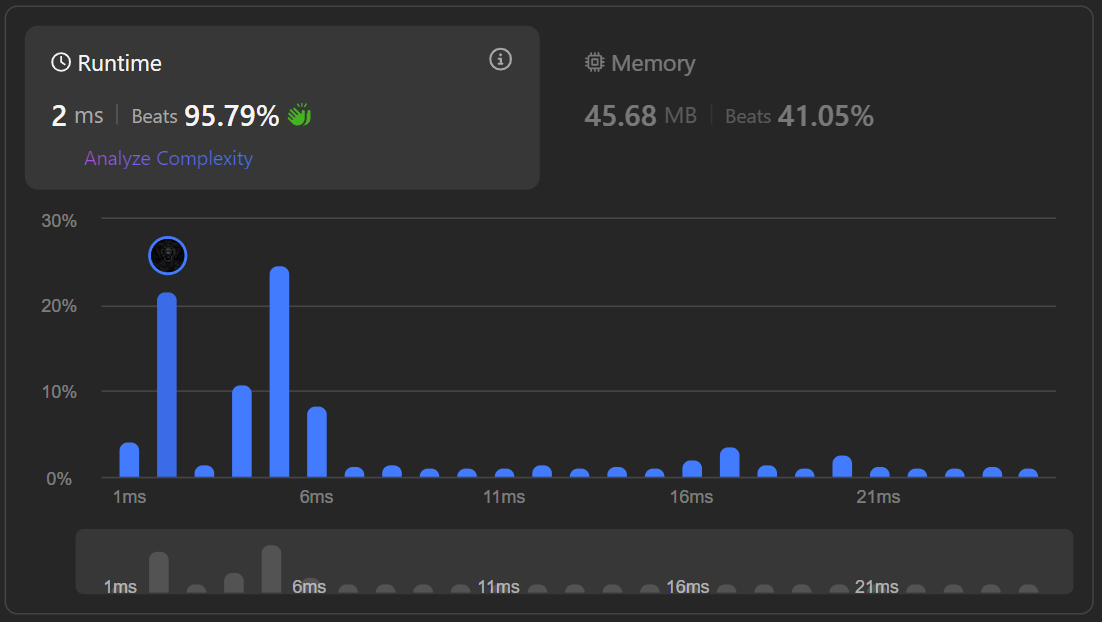

Full Code

class Solution {
    public int[] findThePrefixCommonArray(int[] A, int[] B) {
        // uncomment the approach you want to use
        // return usingSet(A, B);b
        // return usingBitSet(A, B);
        return usingFrequencyArray(A, B);
    }

    // approach 1: Using Set
    private int[] usingSet(int[] A, int[] B) {
        int n = A.length;
        int[] C = new int[n]; // result array

        Set<Integer> setA = new HashSet<>(); // track elements seen in A
        Set<Integer> setB = new HashSet<>(); // track elements seen in B

        for (int i = 0; i < n; i++) {
            setA.add(A[i]); // add current element from A to setA
            setB.add(B[i]); // add current element from B to setB

            int common = 0; // counter for common elements

            // count common elements between setA and setB
            for (int elemA : setA) {
                if (setB.contains(elemA)) {
                    common += 1;
                }
            }

            C[i] = common;
        }
        return C; 
    }

    // approach 2: using BitSet
    private int[] usingBitSet(int[] A, int[] B) {
        int n = A.length;
        int[] C = new int[n]; // result array

        // BitSet to track seen elements (size 2*50 + 1), constraints specify max length is 50
        BitSet bs = new BitSet(101); 

        int common = 0; // counter for common elements

        for (int i = 0; i < n; i++) {
            int aa = A[i]; // current element from A
            int bb = B[i]; // current element from B

            // mark A[i] in BitSet (odd index)
            bs.set((2 * aa) - 1);
            if (bs.get(2 * aa)) { // check if B[i] already set
                common++;
            }

            // Mark B[i] in BitSet (even index)
            bs.set(2 * bb);
            if (bs.get((2 * bb) - 1)) { // check if A[i] already set
                common++;
            }

            C[i] = common;
        }
        return C;
    }

    // approach 3: using frequency array
    private int[] usingFrequencyArray(int[] A, int[] B) {
        int n = A.length;
        int[] C = new int[n]; // result array
        int[] freq = new int[n + 1]; // frequency array to track element occurrences

        int common = 0; // counter for common elements

        for (int i = 0; i < n; i++) {
            // increment frequency for A[i]
            freq[A[i]]++;
            if (freq[A[i]] == 2) { // element appears in both arrays
                common++;
            }

            // increment frequency for B[i]
            freq[B[i]]++;
            if (freq[B[i]] == 2) { // element appears in both arrays
                common++;
            }

            C[i] = common;
        }
        return C;
    }
}