3203. Find Minimum Diameter after Merging Two Trees

---

[Problem]

Tree Depth-First Search Breadth-First Search Graph

---

Tip: Solve Leetcode 1245. Tree Diameter (Unlocked) before attempting this question to gain a foundational understanding.

Intuition

Note: This problem requires understanding tree diameters, which are the longest paths in a tree (undirected acyclic graph).

To minimize the merged diameter:

• Find the diameters of the two trees.
• Connect nodes near the midpoint of each diameter to reduce the overall length effectively.

---

Approach

1. Calculate the Diameter of Each Tree

• Use the two-pass DFS method:
  1. Perform DFS from an arbitrary node to find the farthest node (farthest1).
  2. From farthest1, perform another DFS to find the farthest node (farthest2).
  3. The distance between farthest1 and farthest2 is the tree’s diameter.

public int findDiameter(List<List<Integer>> adjList, int totalNodes) {
    visited = new boolean[totalNodes];
    farthestNode = adjList.get(0).get(0);
    maxDiameter = 0;

    dfs(farthestNode, 0, adjList);

    visited = new boolean[totalNodes];
    dfs(farthestNode, 0, adjList);

    return maxDiameter;
}

2. Merge the Trees

• Calculate the diameters d1 and d2 of tree1 and tree2.
• Connect the middle nodes of both trees to minimize the new diameter:

int r1 = (int) Math.ceil((float) d1 / 2);
int r2 = (int) Math.ceil((float) d2 / 2);
int mergedDiameter = Math.max(d1, d2, r1 + 1 + r2);

3. Determine the Minimum Diameter

• The result is the maximum of the following:

result = Math.max(d1, d2, r1 + 1 + r2);

Warning: If both trees have only one node, handle the edge case where the merged diameter is 1.

Merging Procedure (Example)

Step	Description
1. Tree1 and Tree2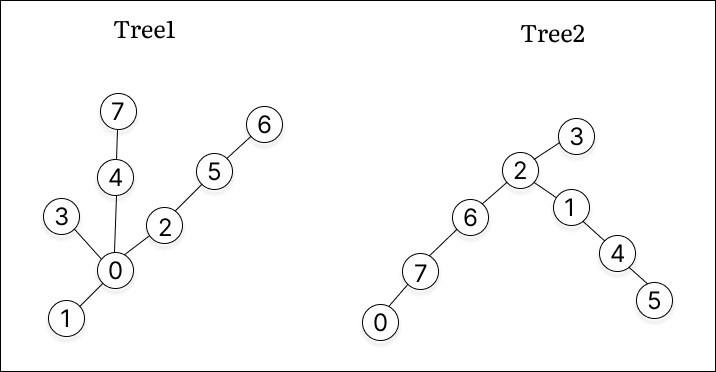
2. Compute Diameters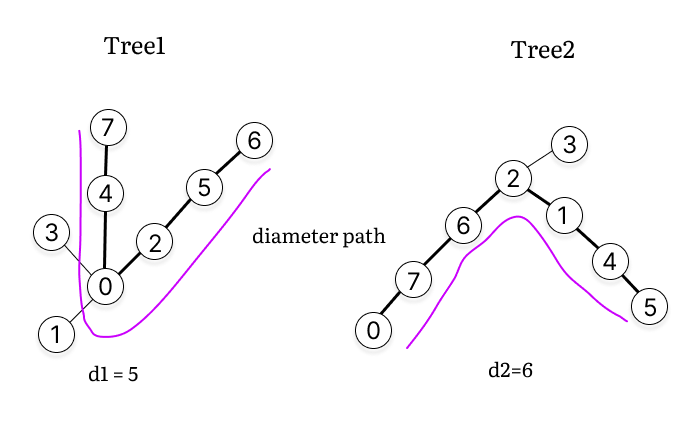
3. Find Middle Nodes
4. Merge Trees
5. Final Merged Tree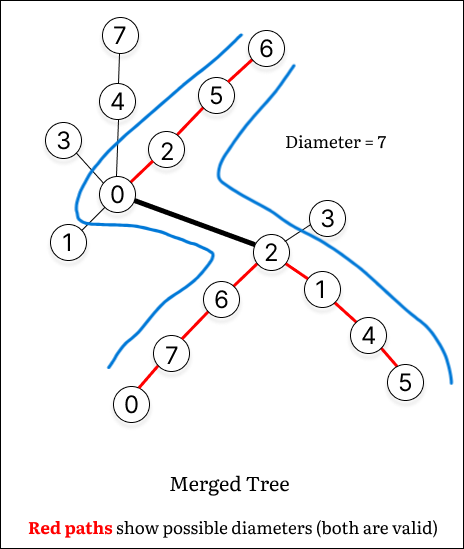

---

Complexity Analysis

• Time Complexity:O(n + m)
  • n and m are the no. of nodes in the two trees.
  • DFS is performed on each tree to calculate the diameter, and merging involves constant-time operations.
• Space Complexity:O(n + m)
  • O(n + m) for storing the adjacency lists of the two trees and stack space of recursive DFS.

---

Code

class Solution {
    private boolean[] visited;
    private int maxDiameter;
    private int farthestNode;

    public int minimumDiameterAfterMerge(int[][] tree1Edges, int[][] tree2Edges) {
        return calculateMinimumDiameter(tree1Edges, tree2Edges);
    }

    public int calculateMinimumDiameter(int[][] tree1Edges, int[][] tree2Edges) {
        int n = tree1Edges.length + 1; // no. of nodes in tree1
        int m = tree2Edges.length + 1; // no. of nodes in tree2

        List<List<Integer>> adj1 = buildAdjList(tree1Edges, n);  // adjacency list tree1
        List<List<Integer>> adj2 = buildAdjList(tree2Edges, m);

        int d1 = n == 1 ? 0 : findDiameter(adj1, n);    // tree1 diameter
        int d2 = m == 1 ? 0 : findDiameter(adj2, m);

        // if both trees have only one node, the merged tree has a diameter of `1`
        if (d1 == 0 && d2 == 0) {
            return 1; 
        }

        // special case where one tree has diameter `1` and the other has diameter `0`
        if ((d1 == 1 && d2 == 0) || (d1 == 0 && d2 == 1)) {
            return Math.max(d1, d2) + 1;
        }

        // calculate the new diameter of the merged tree
        // you can also write `r1 = (d1+1)/2`
        int r1 = (int) Math.ceil((float) d1 / 2); // middle of d1 (r => radius, just for naming convention)
        int r2 = (int) Math.ceil((float) d2 / 2);

        // mergedDiameter is MAX(d1, d2, r1 + 1 + r2)
        int mergedDiameter = Math.max(d1, d2);
        mergedDiameter = Math.max(mergedDiameter, r1 + 1 + r2);

        return mergedDiameter;
    }

    // build adjacency list
    public List<List<Integer>> buildAdjList(int[][] edges, int totalNodes) {
        List<List<Integer>> adjList = new ArrayList<>(totalNodes);
        for (int i = 0; i < totalNodes; i++) {
            adjList.add(new ArrayList<>());
        }
        for (int[] edge : edges) {
            adjList.get(edge[0]).add(edge[1]);
            adjList.get(edge[1]).add(edge[0]);
        }
        return adjList;
    }

    // find the diameter of a tree using two-pass DFS
    public int findDiameter(List<List<Integer>> adjList, int totalNodes) {
        visited = new boolean[totalNodes];
        farthestNode = adjList.get(0).get(0); // arbitrary starting point
        maxDiameter = 0;

        // first DFS to find one endpoint of the diameter
        dfs(farthestNode, 0, adjList);

        // reset visited array and perform DFS from the farthest node to calculate the diameter
        visited = new boolean[totalNodes];
        dfs(farthestNode, 0, adjList);

        return maxDiameter;
    }

    // DFS to find the farthest node and track the maximum distance
    public void dfs(int node, int distance, List<List<Integer>> adjList) {
        if (visited[node]) {
            return;
        }

        visited[node] = true;
        
        if (maxDiameter < distance) {
            // keep updating the max distance and the farthest node
            maxDiameter = distance;
            farthestNode = node;
        }

        for (int neighbor : adjList.get(node)) {
            dfs(neighbor, distance + 1, adjList);
        }
    }
}