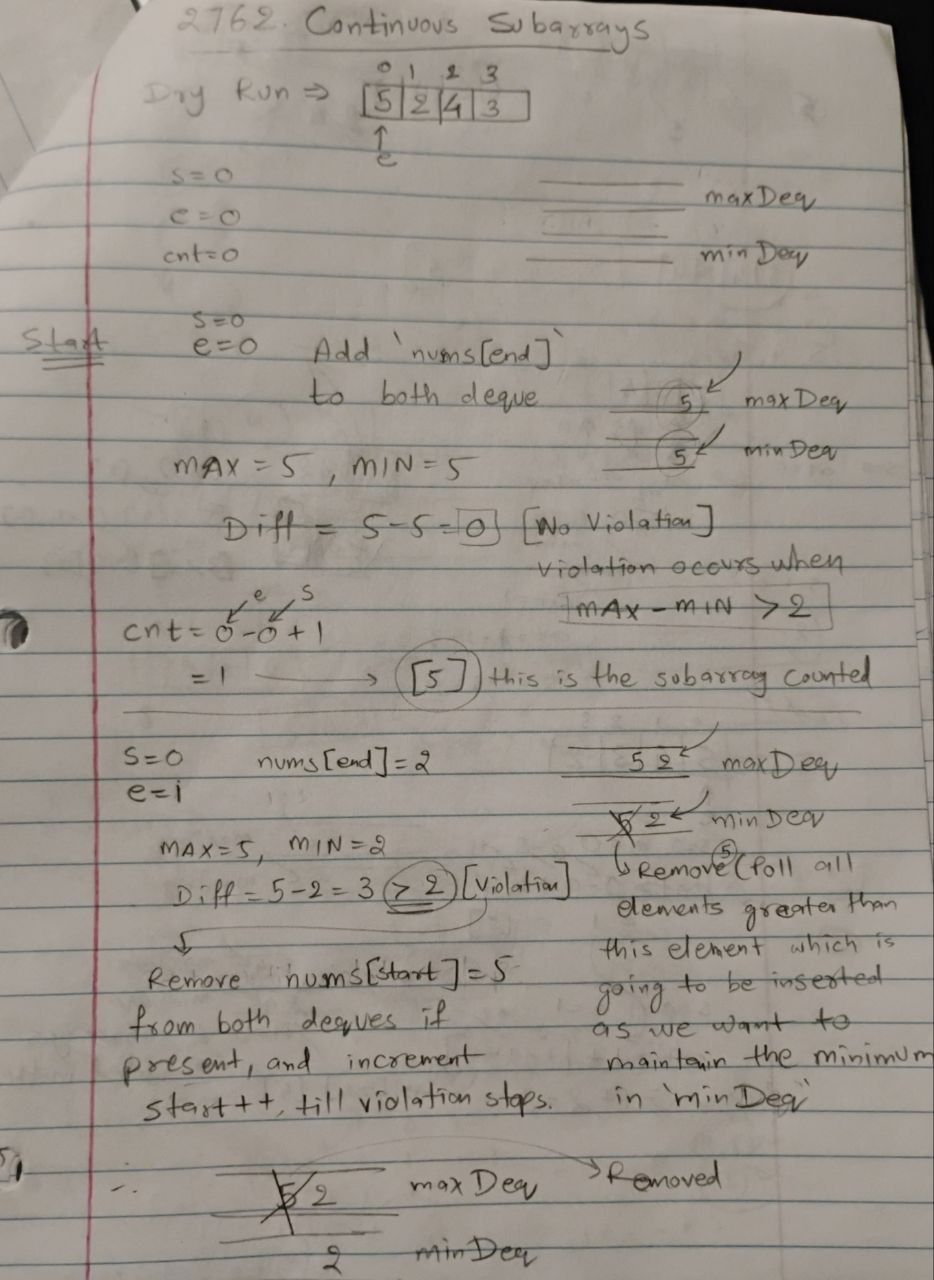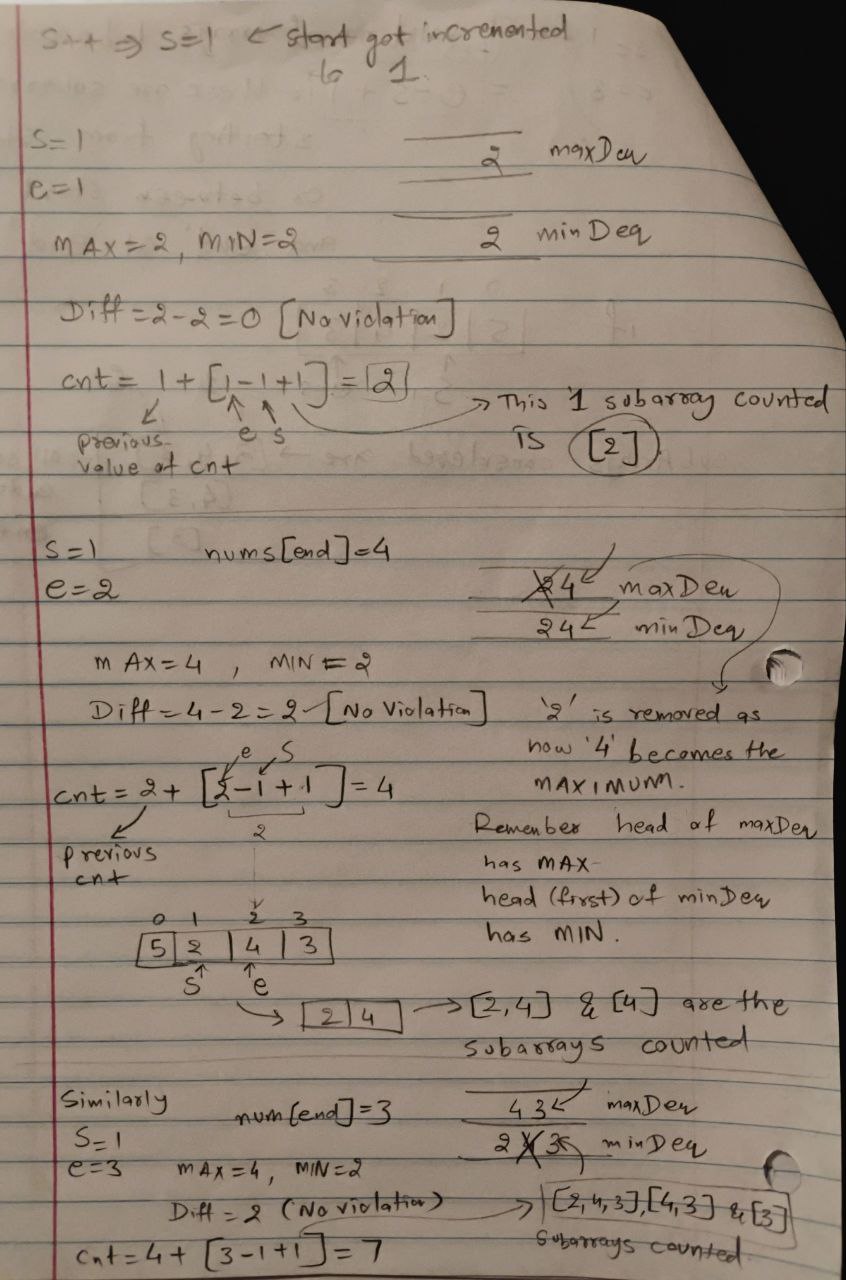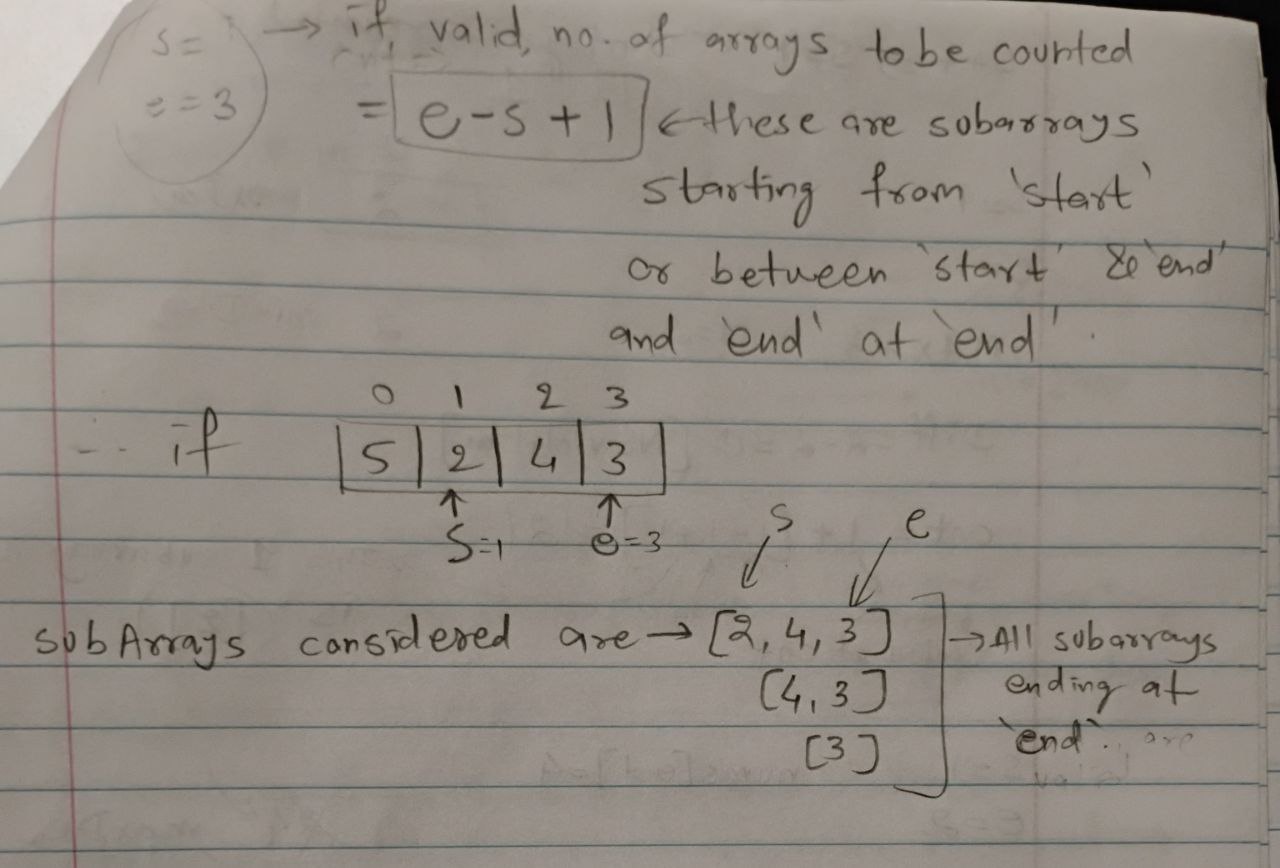2762. Continuous Subarrays

[Problem]

Array Queue Sliding Window Heap(Priority Queue) Ordered Set Monotonic Queue

---

Approach

1. Brute-Force

• The obvious brute-force approach is simple, check all subarrays if they satisfy the condition
• But total subarrays in an n-sized array are n*(n+1)/2, which is order of O(n^2).
• Moreover you iterate through each of them to find whether they are continuous or not.
• This brings the time complexity in order of O(n^3), which is exactly why TLE (Time Limit Exceeded) occurs in leetcode (2129/2135 case).

Here’s the code for the brute-force approach:

// Not preferable O(n^3) solution
class Solution {
    public long continuousSubarrays(int[] nums) {
        int n = nums.length;    
        long count = 0;

        // this approach will take O(n^3) time, hence TLE will occur
        int start = 0;
        for(int end = 0; end < n; end++){
            while(!isCont(nums, start, end)){
                start++;
            }
            count += end - start + 1; // count total valid subarrays for given `start` and `end` pointers
        }

        return count;
    }

    // function to iterate thorugh a subarray to check if it is continuous or not
    public boolean isCont(int[] nums, int start, int end){
        for(int i = start; i <= end; i++){
            for(int j = i + 1; j <= end; j++){
                int diff = Math.abs(nums[i] - nums[j]);
                if(diff > 2){
                    return false;   // condition for continuous array violated
                }
            }
        }
        return true;
    }
}

---

2. A better-approach: Sliding Window with Deque

We utilize a sliding window technique with the help of two deques:

• maxDeq: Maintains the maximum values in the current sliding window.
• minDeq: Maintains the minimum values in the current sliding window.

Steps:

• Iterate with a sliding window (end pointer):
  • Expand the window by adding nums[end] to both maxDeq and minDeq.
• Maintain Monotonic Deques:
  • maxDeq: Ensure elements are in decreasing order by removing smaller elements from the back.
  • minDeq: Ensure elements are in increasing order by removing larger elements from the back.
• Validate the Window:
  • The difference between the maximum (maxDeq.peekFirst()) and minimum (minDeq.peekFirst()) values should not exceed 2.
  • If the condition is violated, shrink the window by incrementing the start pointer and removing the corresponding values from the deques.
• Count Valid Subarrays:
  • For each valid window, the number of subarrays ending at index end is given by: end - start + 1
• Return Total Count:
  • Add count from all valid windows.

---

Complexity Analysis

• Time Complexity:
  • Each element is added and removed from the deques at most once, hence O(n)
• Space Complexity:
  • The two deques require O(n) space in the worst case.

Reference Images

Dry run example [5,2,4,3]

Code

class Solution {
    public long continuousSubarrays(int[] nums) {
        int n = nums.length;
        long cnt = 0;
        
        // Two deques to maintain the maximum and minimum values in the current window
        Deque<Integer> maxDeq = new LinkedList<>();
        Deque<Integer> minDeq = new LinkedList<>();

        int start = 0;

        // Iterate through the array with the `end` pointer
        for(int end = 0; end < n; end++){
            // Maintain decreasing order in maxDeq
            while(!maxDeq.isEmpty() && nums[end] > maxDeq.peekLast()){
                maxDeq.pollLast();
            }

            // Maintain increasing order in minDeq
            while(!minDeq.isEmpty() && nums[end] < minDeq.peekLast()){
                minDeq.pollLast();
            }

            // Add current element to both deques
            maxDeq.offerLast(nums[end]);
            minDeq.offerLast(nums[end]);

            // while the continuous array conditions are violated
            // keep shrinking the window from left, i.e. increment `start`
            while(maxDeq.peekFirst() - minDeq.peekFirst() > 2){
                if(nums[start] == maxDeq.peekFirst()){
                    maxDeq.pollFirst();
                }

                if(nums[start] == minDeq.peekFirst()){
                    minDeq.pollFirst();
                }

                start++;
            }

            // for valid subarray, count all possible subarrays
            // these are all subarrays ending at `end` and starting between `start` and `end` are valid
            cnt += end - start + 1;
        }
        return cnt;
    }
}